
A genetic algorithm (GA) is an optimization algorithm inspired by this process of the survival of the fittest. It belongs to the larger class of evolutionary algorithms (EA). For generations, nature has been a great mentor for humankind. The best of the inventions and the finest of the arts - all are inspired by nature. In the 19th century, Darwin gave the theory of Evolution. The idea that even the most complex of the organisms evolved over generations by the preservation of favorable individual differences and variations and the destruction of those which are injurious, and he called it the “Survival of the Fittest.”
The idea behind this technique is to mimic the biological process of selection, crossover, and mutation and generate the best possible solution over multiple generations.
Before we get into the working of the GA, there are a few terminologies one should be aware of. All these terms are, unsurprisingly, analogous to their biological counterpart.
Population: At any point in time, the set of all the solutions to the present problem (good or bad) are referred to as a population. And all of them reside in a population pool.
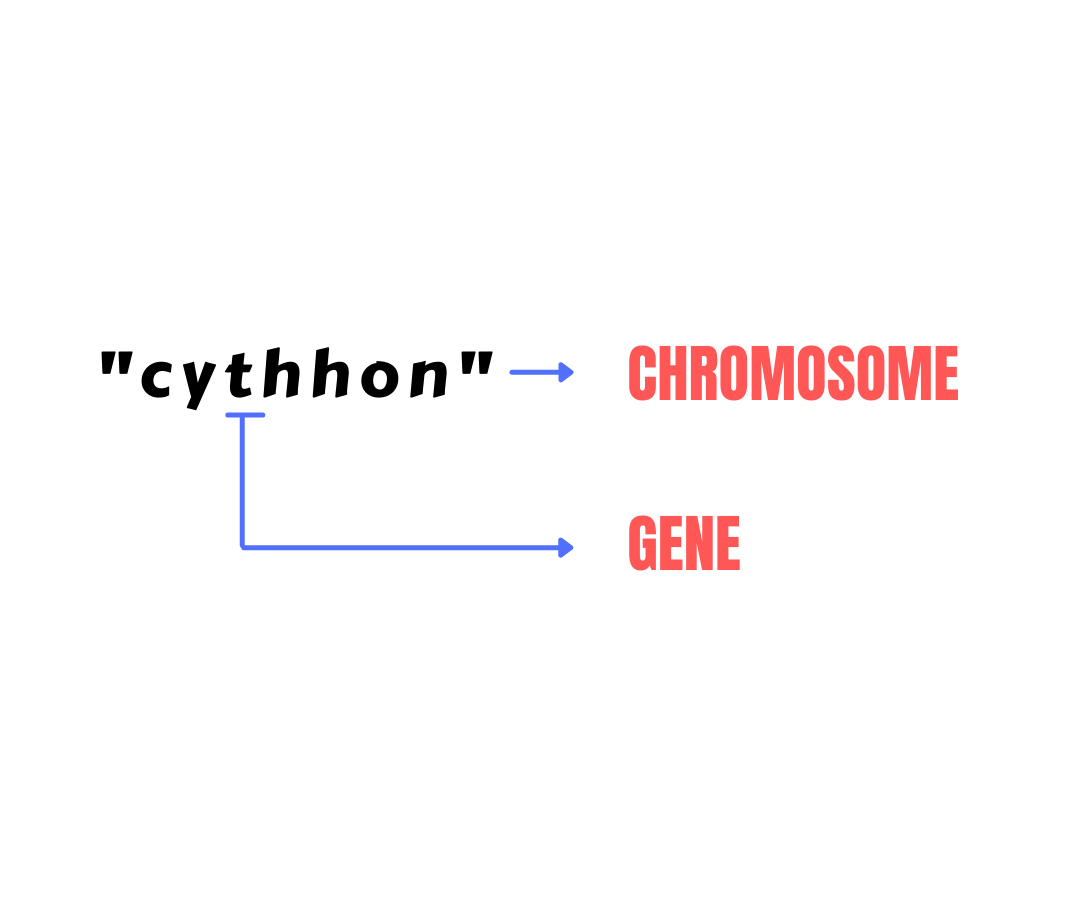
Chromosome: An individual (solution) in the population pool is referred to as a chromosome.
Genes: Gene refers to the elements of a chromosome.
Fitness score: A fitness score is a value assigned to each chromosome, indicating how fit they are (meaning how good a solution is to the given problem). It depends on various factors, and it is calculated by a function called the Fitness function.
Let’s see an example to understand all the terms. Say we have a problem whose solution is the string phytoon. In our population pool, we have some possible solution:
[“abcdefg”, “kadtook”, “phytion”, ”cythhon”] (there may be many more)

All the individuals that are in the population pool (such as cythhon) are called Chromosomes.
Elements of a chromosome (such as c, y, t, h, h, o, and n for cythhon) are called Genes.
The Fitness score is, however, up to us. We define the characteristics that a chromosome must possess to be better than the rest.
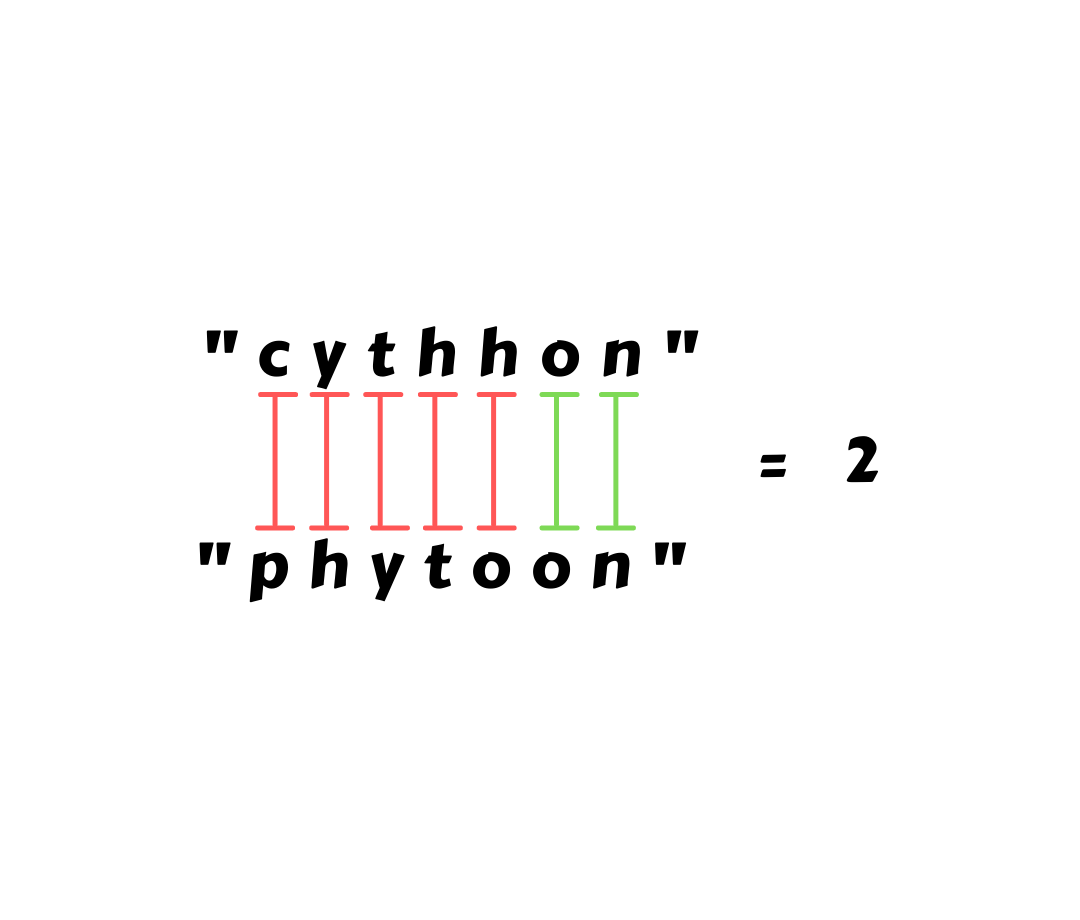
Here let’s say we define the fitness score as how many characters a chromosome has that is at the correct position when compared to the original string phytoon. So, the chromosome:
abcdefg has a score 0,
kadtook has a score 3,
phytion has a score of 6, and
cythhon has a score 2.
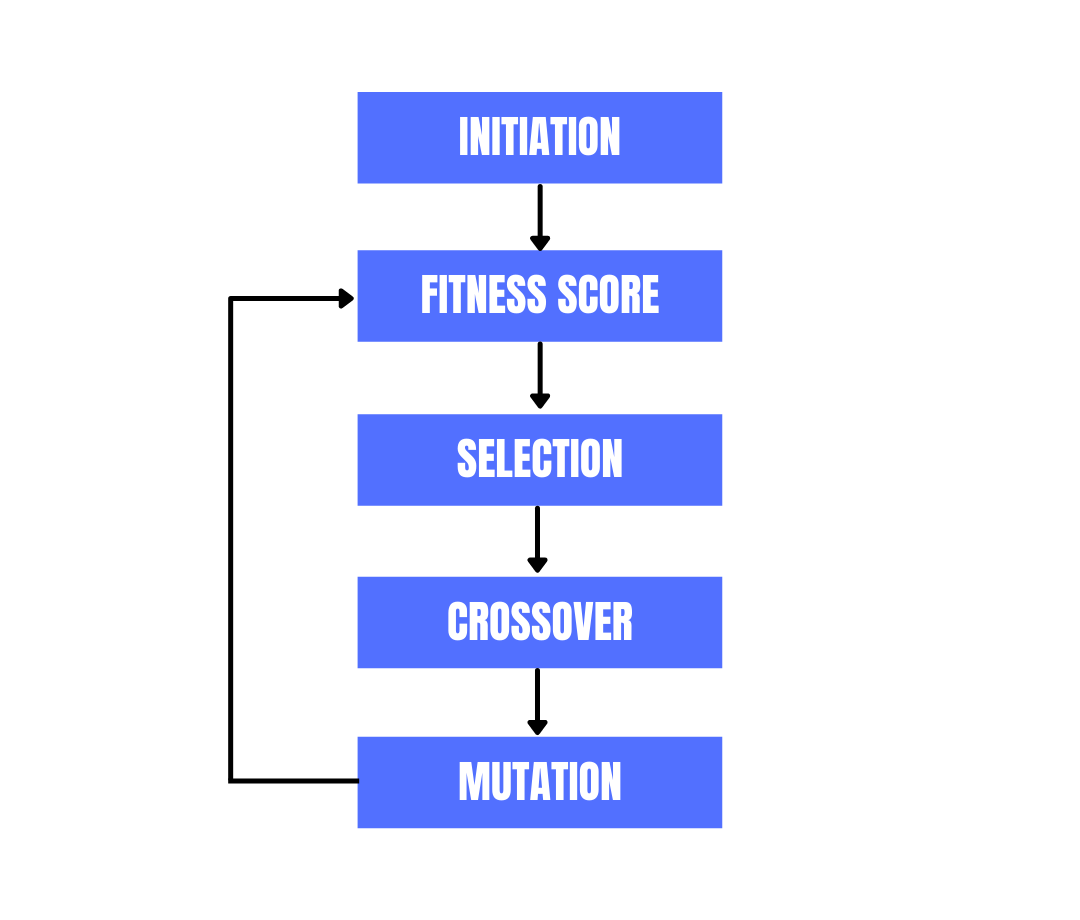
Now we can move on to the actual algorithm. Any solution based on a genetic algorithm follows the following steps:
- Initiation,
- Calculating fitness of the individuals,
- Selection,
- Crossover, and
- Mutation
The first step is the initiation of the population. We generate a pool of possible solutions. The size of the initial population is a parameter itself that can be tweaked to get better results.
After the initiation of the population, the next step is calculating the fitness of the individuals. As we saw earlier, we define a fitness function that calculates the fitness score for each individual.
Now we have a pool of population with individuals where all have a fitness score. The selection process is basically the survival of the fittest. Here we select some individuals that are the ‘fittest’. To do this, there are several ways, but the most common is to take the portion of the population with the highest fitness scores.
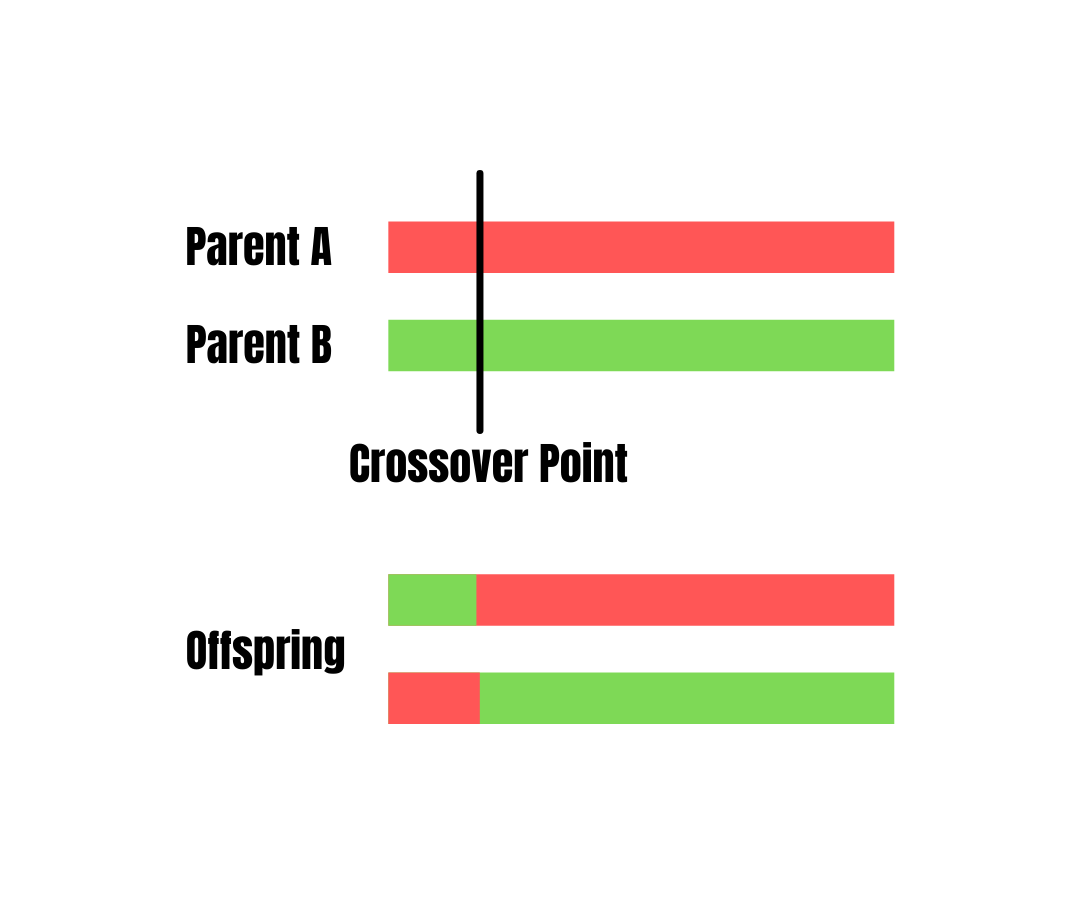
Crossover is analogous to reproduction in nature. The strongest of the individuals survive and reproduce to give birth to offspring containing both parents’ features in a certain amount. The chromosomes selected in the selection process are crossed over to produce offspring. Like the selection process, the crossover can also be done using several methods. The most common is Single Point Crossover, in which a crossover point on the parent organism is selected. All genes beyond that point in the organism are swapped between the two parent organisms.
A mutation is defined as a small and random change in the gene of a chromosome to generate a new individual. Just like in nature, mutation brings variation in the population. It has a low probability of occurring, but it has been observed that the GA must converge.
The steps from calculating fitness score to mutation are repeated. At every cycle, we get a new set of individuals who are referred to as a Generation, just like in nature. For several generations, the average fitness score of the individuals increases until after a point it becomes stagnant, at which point we terminate.
While winding up, let us list the limitations of such an approach. These algorithms are not suitable for simple problems as they can be time-consuming and computationally expensive. We may get stuck at local optima sometimes. Designing a suitable fitness function can be difficult in some cases.

























 Batoi Research Group
Batoi Research Group